Recall our understanding of how computers work with information.



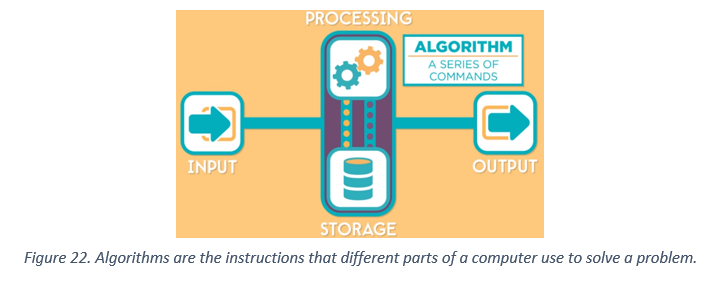
Computers represent all information using zeros and ones. Nobody today actually deals directly with these zeros and ones, but zeros and ones play a big part in how computers actually work. Inside the computer, there are electric wires that carry all the information into the computer.

If you have a wire on which current flows, the signal will be either on or off. The choice is not great, but it is an important start. With one wire, we can present "yes" or "no", "truth" or "lie", "1" or "0", or anything else, which is one of two choices. This "on" / "off" state of the wire is called a "bit" (binary digit). A bit and is the smallest piece of information stored in the computer. If we use more wires, we get more bits. With more zeros and ones - with more bits - we can present information that is more complex.

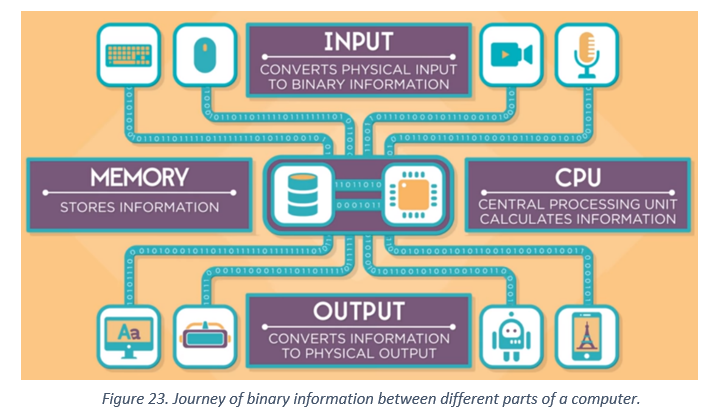
The reason that computers only use two different values is that it is much easier to build devices that do it this way. We could build devices that have ten different levels so that we can use the standard decimal system, but then the devices would be expensive to build since they would need to be very precise.

In the decimal number system, we have ten digits from zero to nine and we have learned already how to count using them.

We can choose to count using a system that uses some other numbers rather than zero to none. Given the "1" or "0" signals that a computer wires carry it seems a very reasonable choice to work in a system that contains only the digits 1 and 0. In the binary number system, we have only two digits: zero and one. With these two digits, we can count to any number.

Here's how it works: in the decimal number system, every position of the figure has different value: units, tens, hundreds and so on. For example, 9 in the position of the hundreds means nine hundred. In the binary system, each position also has a value, but instead of multiplying by 10 each time, multiply by 2. Now we have units, twos, fours, eights, and so on. For example, the number 9 in the binary system is one, zero, zero, one (1001). To convert the value, we calculate (1 x 8) + (0 x 4) + (0 x 2) + (1 x 1) = 9.

The important thing is that ones and zeros can represent any number using a bunch of wires that are “on” or “off”. One bit on its own cannot represent much, so they are usually grouped together in groups of eight, which can represent numbers from 0 to 255. A byte is a group of eight bit. In general, the more wires we use, the greater the number we can store. With 32 wires, you can save everything from 0 to over 4 billion!

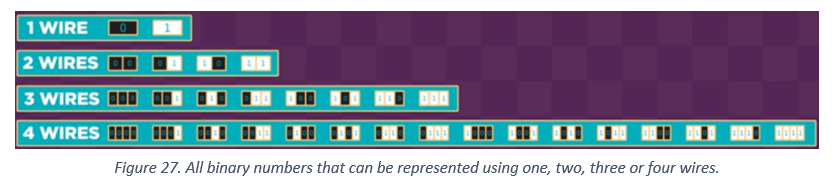
Next, we see a cool trick based on the binary number system.

You ask a group of four of your friends to help in an experiment reading their thoughts. You first hand them a list of 15 numbers and ask them to jointly agree a target number at random from the list. Your friends are then given cards, which contain a jumble of numbers and letters. They stand in a line facing you, cards hidden from your sight. Concentrating on the chosen target number, they transmit their thoughts and you are able to correctly state the chosen number. Read on to find out how the trick is done.

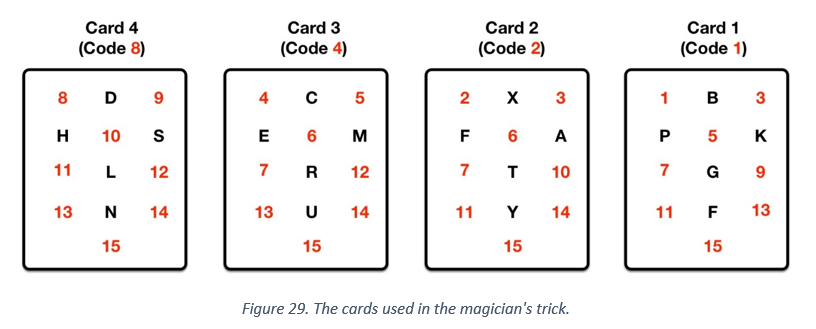
Breaking the magician code

Suppose your friends pick a target number between 1 and 15 at random, say 12. Twelve appears only on cards 3 and card 4 and nowhere else. Now if we add the code numbers that appear on card 3 and card 4, we get 4 + 8 = 12. Adding the code numbers gives the original target number. Try another number, like 6. It appears on cards 2 and 3, which have code numbers 4 and 2, which we add to get 2 + 4 = 6. By knowing what cards a secret number appears on, you can work out from the code numbers what that original secret number was. It always works!

Can you figure out why this trick works?


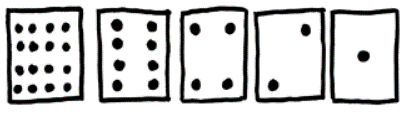
In order to work on this activity, we shall use the following cards to practice building binary numbers.

What do you notice about the number of dots on the cards? How many dots would the next card have if we added a new card?

We can use these cards to make numbers by turning them face down and adding the dots that are showing. Build up each number in the table on the next page using this method. The only rule is that a card has to be completely visible, or completely hidden. When a binary number card is face down, that is, its dots are not showing then it is represented by a zero. When its dots are showing, it is represented by one.

So for example, the number 0 would require that all cards are face down with all dots hidden, resulting in the binary sequence 0000 or just 0. Similarly, the number nine’s representation can be determined as follows.

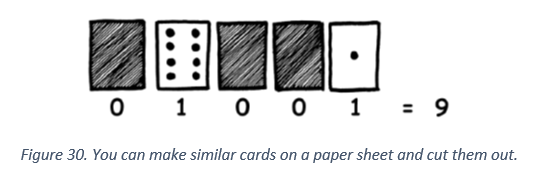
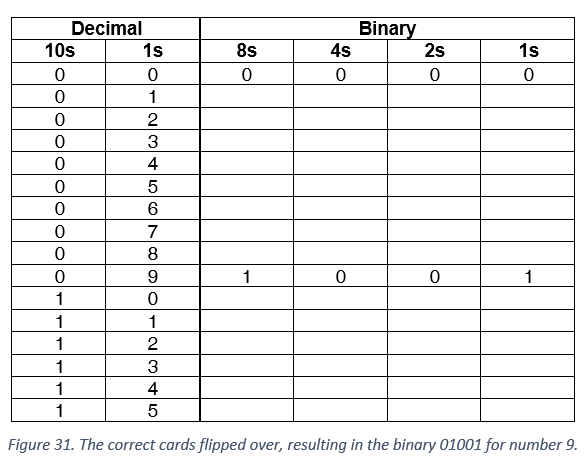
Note that we only end up using the fifth card with 16 dots for decimal numbers greater than 15. What is the largest number we can get with all five cards? Can you work out a logical and reliable method of flipping cards to increase any number by one? Finally, to see that in order to just think about these numbers, we just need two unique symbols, try to work out the following coded numbers:

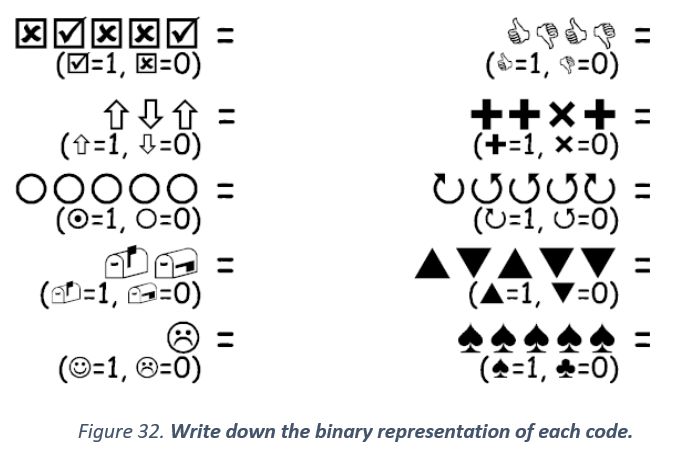
An interesting property of binary numbers is what happens when a zero is put on the right hand side of the number. If we are working in the decimal system, when you put a zero on the right hand side of the number, it is multiplied by 10. For example, 9 becomes 90, 30 becomes 300. But what happens when you put a 0 on the right of a binary number? Try this:

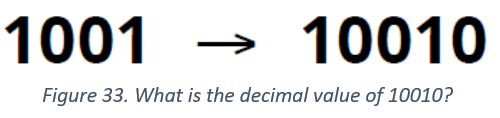
Make up some other numbers to test your answer. Can you figure out a general rule? Finally, let us look at an example of converting a decimal number into binary. We repeatedly divide the decimal number by two. Write down the remainder, which will be either zero or one, and use the quotient as the next value to divide. Keep going until the original number has been divided down to zero. The sequence of remainders is the binary number, except it is in reverse order. As an example, consider the conversion of 1867 to binary in the table below.

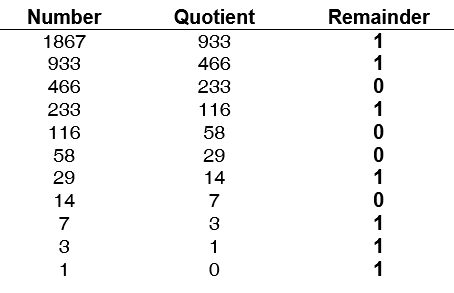
Reading the bits off backwards, we have 111 0100 1011, which we can check by adding up the powers of two: 1024+512+256+64+8+2+1 = 1867.