15.1 Bridging Into Graphs
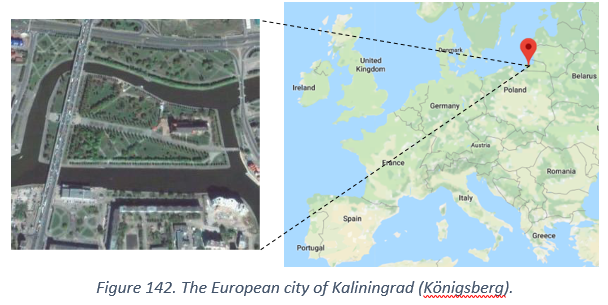
The following satellite image shows the city of Kaliningrad which used to be Königsberg during the 18th century. You can see that the river Pregel surrounds the island in the center of the city. The island is connected to the main land by bridges.
The city actually used to have more bridges, some of which were destroyed during World War II. Below is a map of Königsberg during the 17th century. How many bridges can you identify?
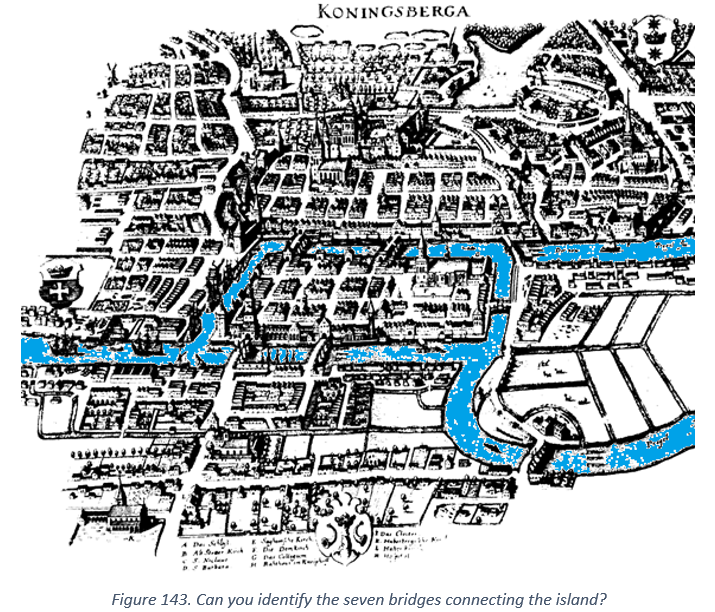
A popular question among the people of the city during the 18th century was “Can someone walk through the city in a way that crosses each bridge exactly once?” Can you find such a way? It is easy to convince someone if you can find such a way. You just show them how to do such a walk. What if you think there is no such way. How would you convince someone that no such walk exists?
This question like many others benefit by developing the right way to think about it. So, for the moment let us put this question on hold and look at another problem. We will come back to the bridges of Königsberg!
15.2 The Muddy City Problem
The Muddy City Problem
Once upon a time, there was a city that had no roads. Getting around the city was particularly difficult after rainstorms because the ground became very muddy -- cars got stuck in the mud and people got their boots dirty. The mayor of the city decided that some of the streets must be paved, but did not want to spend more money than necessary because the city also wanted to build a swimming pool. The mayor therefore specified two conditions:
- Enough streets must be paved so that it is possible for everyone to travel from their house to anyone else’s house only along paved roads,
- The paving should cost as little as possible.
- In the map of the city, the number of paving stones between each house represents the cost of paving that route. Find the best route that connects all the houses, but uses as few counters (paving stones) as possible. What kind of strategies did you use to solve the problem?
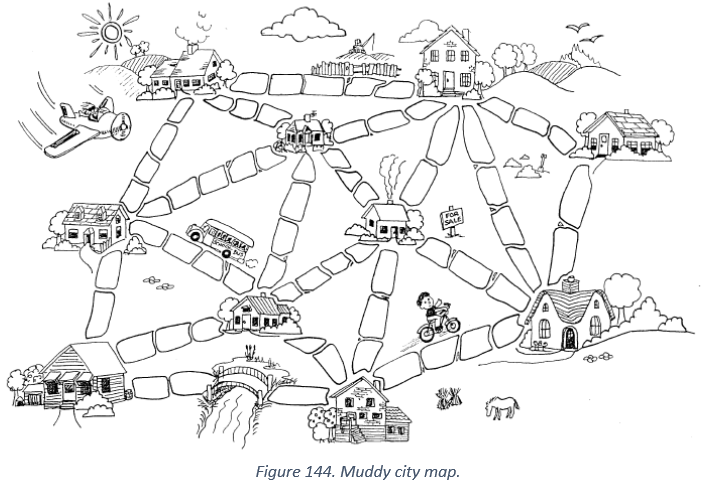
Here is another way of representing the city and the roads.
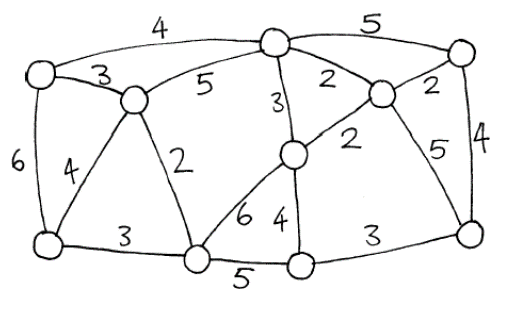
The houses are represented by circles, the muddy roads by lines, and the number besides the line gives the length of a road. Computer scientists and mathematicians often use this sort of diagram to represent these problems. They call it a graph. This may be confusing at first because “graph” is sometimes used in statistics to mean a chart displaying numerical data, such as a bar graph, but the graphs that computer scientists use are not related to these.
The circles are referred to as “vertices” or “nodes” of the graph, the lines connecting the vertices are called “edges”. Each edge has its ends two vertices. The lengths of the edges do not have to be drawn to scale. Many real world problems can be solved by using a graph to represent the problem, such as designing the best network of roads between local cities, or airplane flights around the country.
Muddy City Solution Strategy
One good strategy to find the best solution is to start with an empty map, and gradually add counters until all of the houses are linked, adding the paths in increasing order of length, but not linking houses that are already linked. Different solutions are possible if you change the order in which paths of the same length are added. Try to build your own solutions.
Another strategy is to start with all of the paths paved, and then remove paths you do not need. This takes much more effort though. Make up some of your own muddy city problems and try them out on your friends. Can you find out a rule to describe how many roads or connections are needed for a best solution? Does it depend on how many houses there are in the city?
The Seven Bridges of Königsberg
Let us now return to Königsberg. Recall the problem that we encountered was “Can someone walk through the city in a way that crosses each bridge exactly once?” It should not come as a surprise that our encounter with graphs in the muddy city problem had something to do with this problem as well. The mathematician Leonhard Euler in the year 1736, realized the connection between this problem and the way of thinking about such problems that is today called graph theory.
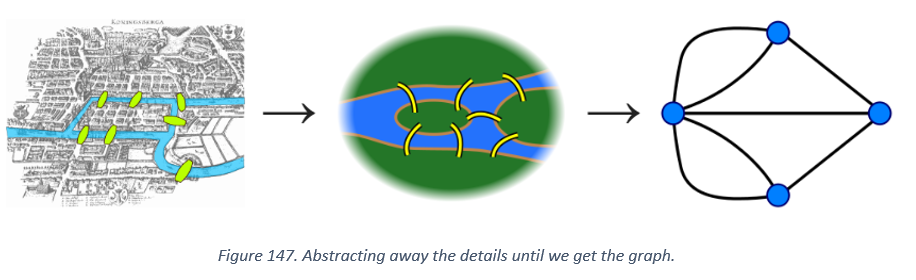
Euler reasoned as follows. He removed the physical nature of the challenge, sketching the town, river and bridges as shown below. There are two important things to observe.
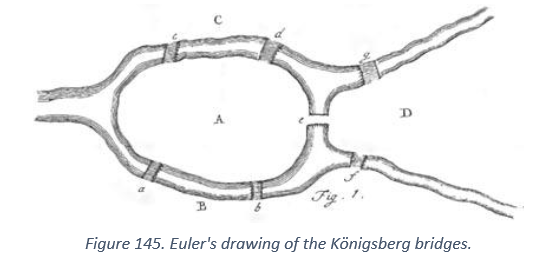
- Abstraction. The idea is to keep information that is important for the problem and forget the remaining information. Size of the landmasses, width of the river, layout of the buildings etc., do not play a part in the solution. As a result, they are removed from the visual description of the problem. This leads to the identification that the problem depends only on the seven bridges connecting four different landmasses.
- Naming Convention. The different pieces of land are labelled A, B, C and D which allows us to distinguish between them. The bridges are labelled a through g. In addition to identification, such a naming convention allows us to describe any walk through the town. For example, A c C g D f B b A, can refer to the walk that starts from A and goes to C through bridge C and then to D through bridge g and so on.
An equivalent but even more simplified visual description of the problem using a graph similar to the Muddy City problem leads us to Figure above
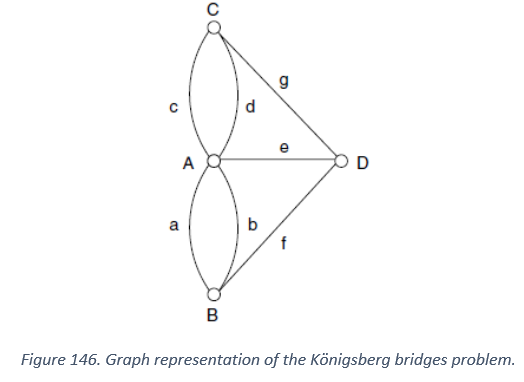
The four vertices of the graph represent the large landmasses, while the edges describe the seven bridges. This reinforces the idea that the solution of the problem depends on the how the different vertices are connected with each other.
We can now play with the simple graph on a sheet of paper and explore different walks. For example, a possible walk starting at B and ending at D, is B a A c C g D e A b B f D. In this walk, three edges meet vertex B, namely a, b, and f; four edges meet vertex A, namely a, c, e, and b; two edges meet vertex C, namely c and g; and three edges meet vertex D, namely g, e, and f. Try out some other walks.
Do you see any pattern?
15.2.1 Solution Strategy
In order to satisfy the requirement of the problem, a traveler in the middle of the journey must enter a vertex through one edge and leave by another. Therefore, that vertex must have an even number of edges. If the traveler at the start of the journey leaves a vertex, then a single edge will be enough and similarly at the end of the journey the traveler again only needs a single edge to reach the end of the journey. The starting and ending vertices then have an odd number of edges.
Note that if the starting and ending point are to be the same vertex, i.e., the requirement that the traveler should end the journey in the same place where it started, then the requirement becomes that all vertices must have an even number of edges.
Given the importance of this property, let us give it a name. The degree of a vertex is the number of edges connected to it.
15.2.2 Degree Property
- In any walk between two different vertices, the starting and ending vertices must have odd degree and all other vertices have even degree.
- In a closed walk or a cycle, (i.e. start and end at the same vertex), every vertex has even degree.
Therefore, we have either exactly two “odd” vertices or all “even” vertices. Can you now give the solution for the Seven Bridges of Königsberg problem?
Observations
We finish our discussion with two observations:
- Note how identifying the degree property simplifies our search for the solution. We no longer have to exhaustively search by trying all the possible walks and hoping that we will get lucky and find the right answer eventually. What if the city had 420 bridges rather than just 7? An exhaustive search would take up too much time even on modern computers. You can think of algorithmic thinking as the search for properties of a given problem that allow us to solve it without having to do an exhaustive search.
- The Königsberg problem ends up not having a solution. How could we convince someone that the problem does not have a solution? Even if they were patient enough to check the results of our exhaustive search, we would still need to convince them that our exhaustive search did not actually miss any case. The degree property allows anyone to perform a quick and simple check that identifies whether a solution exists. This raises the need for being able to “prove” statements about properties that we identify.
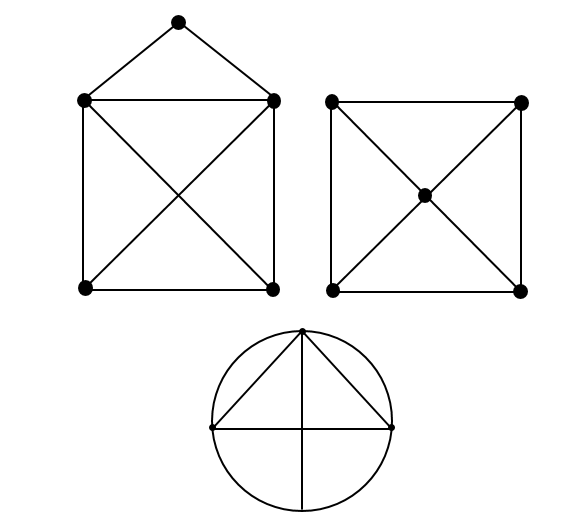
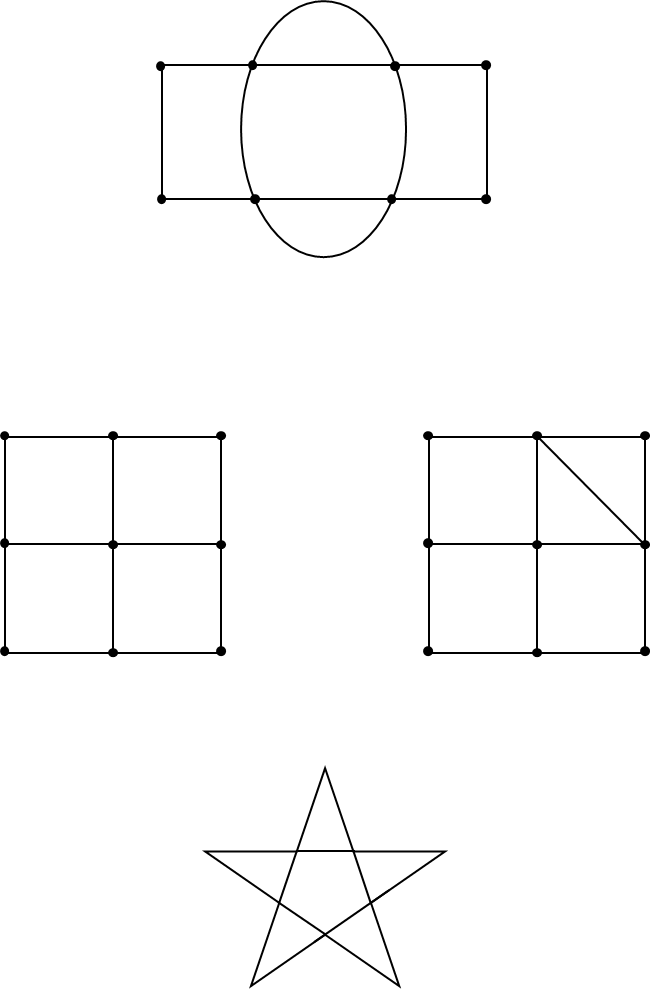
15.3 Excercise
Can you draw these pictures without lifting pen or pencil from the paper, or drawing over the same line twice? Note that folding the paper or drawing additional lines than shown in the image is cheating. Think about what constraint in the Königsberg problem disallows such solutions.